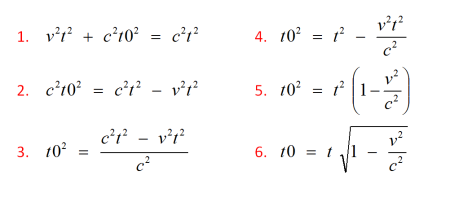Stellen wir uns vor, wir blenden unsere Umwelt aus und konzentrieren uns auf Folgendes:

Wir haben ein Lichtphotonenball in der Hand und lassen diesen fallen. Dieser Ball wird sich mit Lichtgeschwindigkeit gleichförmig und nicht beschleunigend auf die Erde und damit gen Aufprall bewegen. Laut gleichförmiger Bewegung gilt:

Der Weg "s" ist gleich der Geschwindigkeit "v" multipliziert mit der vergangenen Zeit " t ". Für den scheinbar unbewegten Helden gilt daher:

                               s (unbewegt) = v x t

Da es sich um einen Lichtball handelt, wird dieser sich mit der Lichtgeschwindigkeit " c " bewegen:

                               s (unbewegt) = c x t

Um die nachfolgend unterschiedlichen Zeiträume besser unterscheiden zu können, führen wir für unseren Protagonisten, welcher den Ball beobachtet, die Zeit " t0 " ein. Damit ergibt sich für den Fallweg des Lichtphotonenballes:

                                s (unbewegt) = c x t0

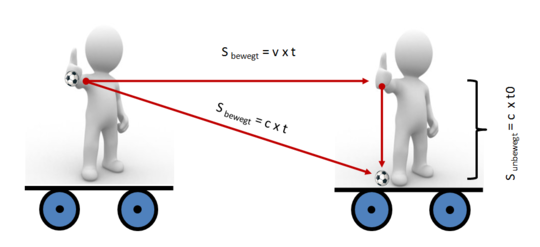
Jetzt stellen wir uns vor unser Held steht auf einen Wagen und wird mit der Geschwindigkeit " v " horizontal bewegt. Aus der Sicht eines Außenstehenden wird er also in der Zeit " t " mit der Geschwindigkeit " v " den Weg " s " zurücklegen.  Wichtig in diesem Zusammenhang, für den Beobachtenden verstreicht die Zeit t. 

                                s (bewegt) = v x t

Der Lichtstrahl selbst wird nun durch diese Bewegung horizontal mitbewegt, was sich auch anschaulich durch folgenden Sachverhalt darstellen lässt:

Lassen wir einen Ball von Burj Khalifa fallen, dann wir dieser nach 13 Sekunden die Erde erreichen. Ein Beobachter sitzt nun wiederum auf einen erdnahen nicht geostationären Satelliten und beob-achtet dies.

Würde sich der Burj genau am Äquator befinden, dann würde sich das Bauwerk in diesen 13 Sekunden um rund 6km bewegt haben. Aus Sicht des Beobachters ist der Weg des Balles nicht vertikal sondern durch die Erdrotation eher diagonal. Der Ballwerfende erkennt dies freilich aus Mangel an Bezügen nicht.

Der analoge diagonale Weg unseres Lichtballes beträgt also aus Sicht des Beobachters, welcher das bewegte System beobachtet:

                                s (bewegt) = c x t

Dabei ist wichtig, das hier die Zeit des Beobachtenden zählt, welche wir ebenfalls mit t beschreiben wollen. Vom Fall des Balles bis zum Aufschlag gilt selbstverständlich auch hier, dass das Licht sich mit c bewegt. Der Weg nun allerdings diagonal:

Wir suchen nun die Zeit t0 um festzustellen, wie diese in Relation zum Beobachter liegt. Das gelingt uns mit ein wenig Mathematik durch Anwendung des Satzes von Pythagoras:

Im Nachfolgendem kann man den Wurzelausdruck reduzieren, wenn man die Geschwindigkeit v zur Lichtgeschwindigkeit ins Verhältnis setzt. Wir wollen dies tun für:

                                                                   v = 10   % c

                                                                   v = 20   % c

                                                                   v = 30   % c

                                                                   v =  ...   % c

                                                                   v = 100 % c

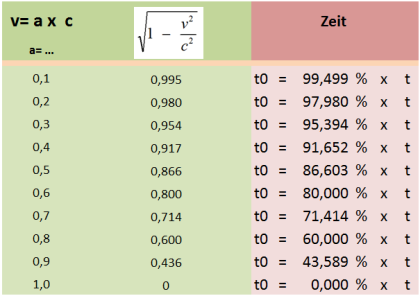
           Wie ist diese Tabelle zu interpretieren?

Nehmen wir an, wir bewegen uns mit 50% der Lichtgeschwindigkeit, dann wird die Zeit für uns im Raumschiff nur 86,603% der Zeit des Beobachters verstreichen, welcher sich in Relation zu unserem Raumschiff im Zustand der Ruhe befindet. 

Vergehen also beim Beobachter 100 Jahre, dann werden wir nur um 86,6Jahre gealtert sein. 

Aus der Tabelle ist auch erkennbar, dass beim Erreichen von Lichtgeschwindigkeit aus Sicht des Beobachters die Zeit im Raumschiff stehen geblieben scheint.

Aus unserem letzten Beispiel "Autorennen" erkannten wir das Grundprinzip, jedoch ist dort der Unterschied der Zeiten bei halber Lichtgeschwindigkeit genau die Hälfte.

Das Beispiel Autorennen beschreibt also Einstein nicht umfassend genug.

Dieser Effekt wird Zeitdiladation genannt!