1. Bildentsehung im Fernrohr  - Vom Objekt zum reellen Zwischenbild

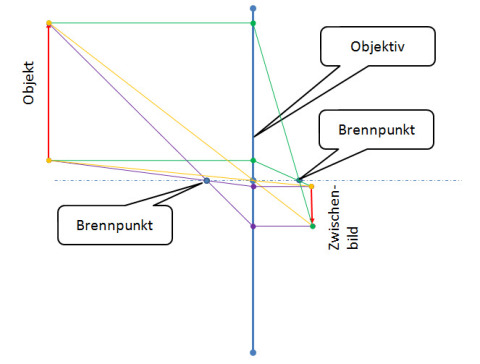
Frontseitig am  Refraktor (Linsenteleskop) befindet sich das Objektiv. Dieses ist durch zwei Kenngrößen gekennzeichnet. Zum einem ist dies die Brennweite. Dies ist der Abstand vom Objektiv, in welchem parallel einlaufende Strahlen in einem Punkt gebündelt werden. Für die Entstehung (Konstruktion) eines Bildes sind drei Strahlen heranzuziehen:

A:           Der Parallelstrahl                            (grün)

B:           Der Mittelpunktstrahl                       (gelb)

C:           Der Brennpunktstrahl                     (violett)

Im Objektiv wird aus dem:

A:           Der Parallelstrahl             ein                                        Brennpunktstrahl           (grün)

B:           Mittelpunktstrahl              unverändert ein                     Mittelpunktstrahl           (gelb)

C:           Brennpunktstrahl             ein                                         Parallelstrahl                (violett)

Wie man in der Abbildung erkennt und erwähnt wurde, ist der Brennpunkt der Punkt, an dem der parallel eintreffende „Parallelstrahl“ die optische Achse schneidet.

Das entstehende Bild ist seitenverkehrt und wird in der Literatur oft als reelles Zwischenbild bezeichnet. Das hängt damit zusammen, da dieses Bild abbildbar ist und entweder auf einen Schirm sichtbar gemacht oder fotografiert werden kann (fokale Fotografie).

Was man erkennt ist, dass sich das Bild hinter dem Brennpunkt aufbaut. Wenn man sich die gängigen Definitionen eines Fernrohres ansieht, dann wird dort explizit erwähnt, dass sich dieses Bild im Brennpunkt abbildet. Das scheint im Widerspruch zu dem  gerade Beschriebenen zu stehen.  

Vom Objekt zum reellen Zwischenbild im Fernrohr

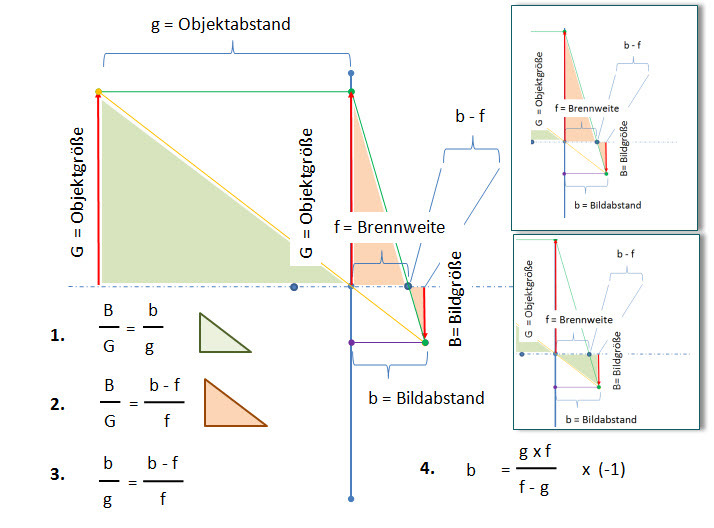
Im Unterschied zur vorangegangenen Darstellung befinden sich astronomische Objekte in sehr weiter Entfernung. Aus dem Bild lassen sich über Strahlensätze Gesetzmäßigkeiten ableiten, die es ermöglichen, folgenden Satz zu beweisen:

• Sehr weit entfernte Objekte haben Ihr Zwischenbild immer in der Brennweite des Teleskopes und das unabhängig von deren Größe.

Diesen Zusammenhang beschreibt die sogenannte Linsengleichung. Da die linken Seiten der Gleichungen 1 und 2 gleich sind, müssen auch die rechten Seiten identische Ergebnisse liefern. Dies führt zur Gleichung 3.  Die entsprechenden Strahlensatzdreieicke sind auf dem Bild vergrößert dargestellt. Gleichung 4 ergibt sich aus Umformung der Gleichung 3.  Was bedeutet dies:

Beispiel:

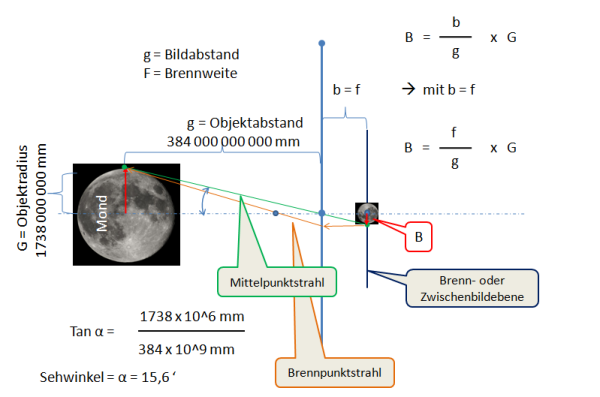
Wir suchen den Ort des Zwischenbildes eines astronomisch nahen und großen Objektes; den Mond. Wie in der Gleichung 4 ersichtlich spielt die Größe dabei keine Rolle. Lediglich die Brennweite des Teleskopes und die Entfernung spielen eine Rolle.

Ergebnis:

Das Zwischenbild befindet sich 0,0000007 mm (!) hinter dem Brennpunkt des Objektivs! Nachfolgend das Excel Ergebnis. Die Heranziehung des Parallelstrahles für die Linsengleichung scheint zur Annahme zu führen, dass diese Gleichung nur funktionieren kann, wenn der Objektivdurchmesser gleich dem Monddurchmesser ist (siehe vorangehendes Bild). Mathematisch und in der Theorie ist dies korrekt und führt zu einem richtigen Ergebnis. Praktisch gesehen ist dies natürlich unrealistisch. Das Modell behält trotzdem seine mathematische Richtigkeit. Der Parallelstrahl steht im wahren Leben unter einem Winkel von 89,9999835° zur optischen Achse und ist also nahezu parallel zur Bildebene.

Fazit: 

Fokale Astrofotographie bringt den Chip in den Brennpunkt des Objektives, um das Zwischenbild aufzunehmen. Dabei liegt das aufzunehmende Zwischenbild bei sehr weit entfernten Objekten im Fernrohr im Brennpunkt des Objektives. Je weiter entfernt ein Objekt, desto näher komme ich an diesen Punkt heran, ohne das er jemals erreicht wird (Unendlichkeit).

Ein weiterer Punkt, welcher in der Literatur erwähnt wird ist, dass die Strahlen unendlicher Objekte parallel einfallen. Das ist einfach erklärt.  Je weiter ein Objekt entfernt ist, desto kleiner werden die Winkel zwischen parallel einfallenden Strahlen und Brennpunkt- und Mittelpunktstrahlen. Das ist bereits am Bild mit etwas Phantasie leicht nachvollziehbar. Befindet sich ein Objekt in der Unendlichkeit, dann ist der Winkel unendlich klein, was bedeutet, dass die Strahlen keinen Schnittpunkt mehr aufweisen. Sie sind parallel. 

Die Unendlichkeit ist ein schwer greifbarer Begriff und so lohnt ein Blick auf das bereits Erwähnte, den Mond.  Um es ein wenig einfacher zu gestalten, nutze ich den bereits erwähnten Zusammen-hang:

„Der Schnittpunkt aller Strahlen schneidet sich bei sehr weit entfernten Objekten im Brennpunkt des Objektivs“

Beispiel Mond:

Vorab eine Zusammenfassung.

• Alle Strahlen eines weit entfernten Objektes werden in der Brennpunktebene des Objektivs gebündelt, was bereits erklärt wurde. So rückt die Zwischenbildebene des Mondes bereits auf 0,0000007 mm an den Brennpunkt heran
• Bisher wurde das Zwischenbild immer durch die Schnittpunkte zweier Strahlen gebildet
• Kennt man die Lage des Zwischenbildes genügt ein Strahl, denn auch die Zwischenbildbene schneidet den Schnittpunkt aller Strahlen und die Lage kennen wir, sie ist bis nahezu identisch mit der Brennpunktebene (siehe ersten Punkt)
• Für das Erzeugen eines Zwischenbildes genügt daher ein Strahl, welcher sich mit der Ebene lotrecht zum Brennpunkt schneidet
• Als Strahl dafür nutzen wir den Mittelpunktstrahl
• Als erstes bildet man also die Ebene durch den Brennpunkt
• Als Zweites trägt man den Mittelpunktstrahl vom Rand  des Objektes auf
• Beide schneiden sich und bilden das Abbild des Objektrandes
• es ist jetzt auch möglich, die anderen Strahlen einzuzeichnen, indem man vom Schnittpunkt des Mittelpunktstrahles mit der Brennpunkt- bzw. Zischenbildebene die Strahlen "rückwärs" einzeichnet. (Siehe Brennpunktstrahl im Bild)

Unter welchem Winkel trifft nun ein Lichtpunkt am Rand des Mondes auf das Objektiv?

Das Ergebnis sind rund 16‘ von der optischen Achse bis zum Rand. Für die gesamte Mondscheibe sind dies 32'  Was einen Astrofotografen eher interessieren dürfte ist das Abbild des Mondes bei einem gegebenen Teleskop:

Aus der Gleichung für B kann man nun die icht wirklich hilfreiche Winkelagabe in mm umrechnen, was bedeutet, dass dies eine greifbare Angabe für die Größe auf einem Foto ist:

Was hier bereits erkennbar ist. Ein Objekt erzeugt ein Zwischenbild, wenn es eine Ausdehnung hat, unter welcher es beobachtet wird. Aufgrund Ihrer Entfernung lassen sich Sterne deshalb nicht vergrößern. Eine Ansammlung von Sternen wiederum schon, da diese am Himmel als flächenhaftes Objekt erscheinen. Dabei vergrößere ich im eigentlichen Sinne den Raum zwischen den Sternen.

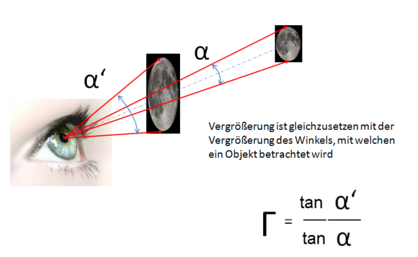
Um eine Vergrößerung zu erreichen, muß ich also das Objekt näher an das Auge bringen. Dies wird durch eine Vergrößerung des Sehwinkels erreicht.

Bisher haben wir lediglich ein Zwischenbild und dessen Größe ist nur von der Brennweite des Teleskopes abhängig, wie in der Gleichung im Bild "Mond - Sehwinkel und Zwischenbildgröße" erkennbar ist. Dieses Bild kann weiter vergrößert werden, indem man es (da reell) mit einer Lupe vergrößert. Die entsprechende "Lupe" in einem Teleskop ist das nachgeschaltete Okular.

Im nachfolgenden Kapitel wird beschrieben, wie man zu einer Objektvergrößerung kommt.