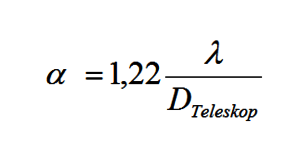4. Das Auflösungsvermögen von Teleskopen
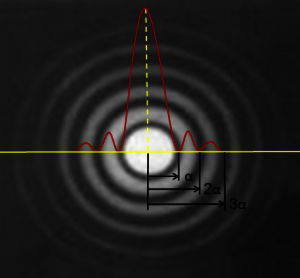
In einem vorangegangenen Kapitel hatte ich beschrieben, dass Sterne nicht vergrößerbar sind und als Punkt im Zwischenbild abgebildet werden. Tatsächlich handelt es sich nicht um einen Punkt sondern um kleine konzentrische Scheiben, welche Bereiche maximaler Helligkeit und maximaler Dunkelheit haben. Diese Scheibchen nennt man Beugungsscheibchen.
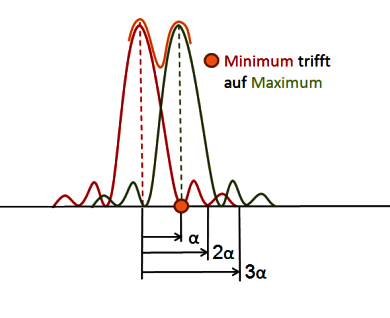
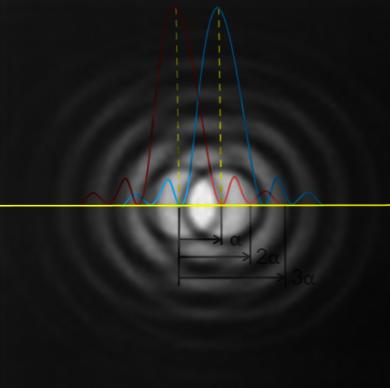
Liegen nun zwei Sterne eng beieinander, dann beschreibt das Auflösungsvermögen, ob diese beide Sterne voneinander getrennt erscheinen. Dies ist der Fall, wenn das Helligkeitsmaximum des einen Sterns mit dem ersten Helligkeitsminimium des zweiten Sterns zusammentrifft. Diesen Zusammen-hang nennt man Rayleigh Kriterium.
"Zwei punktförmige Lichtquellen können gerade noch getrennt unterschieden werden, wenn das zentrale Helligkeitsmaximum des Beugungsscheibchen des ersten Objektes mit dem ersten Minimum des zweiten Objektes zusmmenfällt"
Am Besten wird dies nachvollziehbar, indem man ein kleines Gedankenexperiment vollzieht. Dazu lässt man zwei Steine mit einen Abstand x ins Wasser fallen. Das verdängte Volumen wird aus dem Wasser herausgeschleudert. Erkennt man aus der Form dieser Reaktion, das zwei Steine ins Wasser fielen, dann hat man beide Objekte getrennt darstellen können.
Aus der ersten Graphik erkennt man, dass damit der Abstand zwischen zwei identischen Objekten Alpha sein muss, damit das Raileigh Kriterium efüllt ist. Dieser Abstand ist identisch mit dem Sehwinkel, welcher berechnet werden kann:
Mit:
- Alpha = Sehwinkel / Auflösung Teleskop [rad]
- Lambda = Beobachtungswellenlänge [m]
- D = Objektivdurchmesser [m]
Wichtig hierbei sind folgende Erkenntnisse:
- große Durchmesser liefern kleine Alpha also kleine Beugungsscheibchen
- kleine Durchmesser liefern große Alpha also große Beugungsscheibchen
- es ist logisch, dass man besser auflösen kann, wenn die Scheibchen klein sind, denn dann werden die im Bild "Rayleigh Kriterium" dargestellten Helligkeitskurven schmal und gegebenenfalls entsteht sogar ein schwarzer Zwischenraum zwischen zwei Sternen
- Sind die Scheibchen groß (kleine Durchmesser), lassen sich keine Sterne erkennen. Das ganze Bild ist ein breiiger Match aus diffuser Helligkeit
Die Gleichung wurde im Übrigen bereits beim Thema "Das Sichtbarmachen flächiger Objekte hergeleitet". Sie entspricht dem Radius des Beugungsscheibchens. Alpha entsprach dort "Beta / 2".
Das menschliche Auge kann Wellenlängen von 380 bis 750 x 10^(-9) m Wellenlänge wahrnehmen, so dass man üblicherweise für Lambda den Mittelwert annimmt, welcher ca. bei 530nm oder 530 x 10^(-9) m liegt.
Somit wird es möglich zu berechnen, welche Objekte in welchen Beobachtungswinkel zueinander stehen müssen, damit man sie noch als zwei Objekte erkennbar sind.
Für unser SC bedeutet das:
D Teleskop = 203,2 x 10^(-3) m
Lambda = 530 x 10^(-9) m
Alpha = 3,18 x 10^(-6) = 0,00018° = 0,011' = 0,656''
Durch eine einfache Trigonometrie lässt sich bei einer Mondentfernung von 384 000 000m der Abstand auflösbarer Objekte berechnen:
x = tan 0,00018° x 384.000.000m = 1.221m
Mit unserem SC lassen sich also Objekte auflösen, welche auf dem Mond einen Abstand von 1,22km haben.