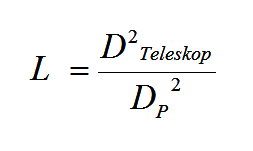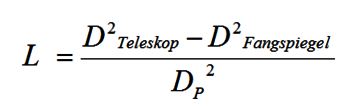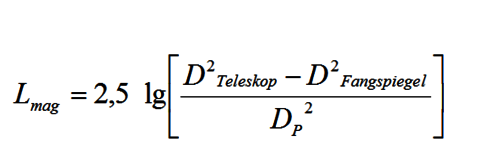3. Das Sichtbarmachen punktförmiger Objekte
In den vorangegangenen Kapiteln wurde beschrieben, dass ein Teleskop nicht nur vergrößern, sondern auch Dinge sichtbar machen soll, welche dem Auge sonst verborgen bleiben. Dabei ist von Bedeutung, wie viel Licht ein Teleskop sammeln kann. Dieses Eigenschaft nennt man Lichtsammel-vermögen. Es gibt Auskunft darüber, wieviel Licht ein Teleskop mehr sammelt als das menschliche Auge.
Im vorangegangenen Kapitel zum Thema flächenhafte Objekte haben wir uns schon mit den drei wichtigsten Kenngrößen vertraut gemacht:
Die Brennweite ist für die Größe des Zwischenbildes verantwortlich auf dessen Fläche sich die Lichtinformationen verteilen, welche in ihrer Quantität vom Objektivdurchmesser abhängen. Diese Information wird mittels Okularen in ein Lichtbündel überführt, welches sich Austrittspupille nennt. Je nachdem wie ich die zwei Zwischenbildinformationen vergrößere, desto heller oder dunkler erscheint das Ergebnis in Ahängigkeit der Austrittspupille.
Fraglich ist nun, ob die Kenngrößen bei punktförmigen Objekten ebenfalls Ihre Berechtigung haben.
Zu allererst muß man sich klarmachen, dass der scheinbare Durchmesser von Sternen zum überwiegenden Teil zu Blickwinkeln führt, welche unter 0,01'' Bogensekunden liegen. Sie sind also winzigste Scheibchen und nicht als solche wahrnehmbar.
Im Zwischenbild des Teleskopes werden sie als Beugungsscheibchen dargestellt. Die Größe dieser Scheibchen wurde schon in im Thema maximale Vergrößerung in Winkelsekunden berechnet. Dies sagt noch Nichts über deren lineare Ausdehnung aus. Diese ist selbstverständlich wiederum von der Brennweite abhängig.
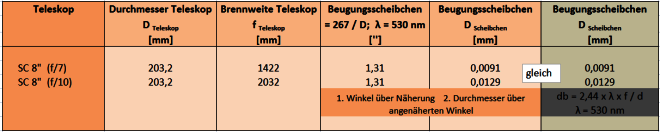
Um eine Vorstellung zu bekommen, wie groß so ein Scheibchen ist anbei ein Beispiel:
Man erkennt, dass der Unterschied zwischen dem Öffnungsverhältnis f/7 und f/10 zu einem Unterschied führt, welcher ca. 4µm beträgt. Das ist unbedeutend wenig. Die Zwischenbildgröße ist aber für die Vergrößerung und damit für die Austrittspupille von Bedeutung. Real gesehen sind diese Zwischenbilder Punkte und auch durch vergrößern werden diese Scheibchen erst oberhalb der maximalen Vergrößerung zu Scheibchen im Okular.
Dies bedeutet, dass das Licht, welches ein Teleskop bei Fokussierung auf einen einzelnen Stern sammelt auf ein winziges Zwischenbild dieses Sterns verteilt wird. Ob dieses Zwischenbild nun 4µm größer oder kleiner ist spielt praktische keine Rolle. Beide Zwischenbilder sind praktisch gleichgroß und gleichhell und damit verliert die Brennweite Ihre Bedeutung.
Was hingegen hier entscheidend wird ist die Öffnung, denn das Licht wird nun nicht mehr auf "große" Zwischenbildflächen (wie bei flächigen Objekten) verteilt sondern nahezu in einen Punkt vereinigt.
- Große Öffnung bedeutet viel Licht auf einen Punkt konzentriert
- Kleinere Öffnung bedeutet weniger Licht auf einen Punkt konzentriert
Auch hier wiederum ein kleines Gedankenexperiment. Ich nehme zwei Trichter und stelle diese mit der engen Öfnung auf ein Blatt Papier. Ein Trichter hat eine große Öffnung (= großer Teleskop-öffnung) und der andere eine kleine Öffnung (= kleinerer Teleskopöffnung). Beide haben aber eine identische minimale Öffnung, was den nahezu gleich großen, besser winzigen Beugungsscheibchen entspricht. Nun streue ich Sand über Beide. Beim Trichter mit der kleinen Öfnung wird viel Sand neben dem Trichter landen. Beim Trichter mit der größeren Öffnung wird dieser Verlust kleiner sein. Hebe ich beide Trichter vom Papier, und zähle die Sandkörner im begrenzenden Kreis der kleineren Trichteröffnung, dann wird dort im großen Trichter mehr zu finden sein als im Trichter mit der kleineren Öffnung.
Das wiederum führt zur Gesetzmäßigkeit:
- Das Lichtsammelvermögen ist nur von der Fläche (Durchmesser) der Optik beeinflusst!
Bildet man das Verhältnis dieser Fläche zur Fläche der Augenpupille, dann ergibt sich die Abhängigkeit der Durchmesser im Quadrat.
L = Lichtsammelvermögen
D Teleskop = Durchmesser des Teleskopobjektives
DP = Augenpupille Durchmesser
Da die menschliche Pupille sich maximal auf 7mm weiten kann, kann man für DP 49mm2 ansetzen.
Bei bestimmten Teleskopen steht desweiteren nicht die komplette Objektivöffnung als Lichtsammler zur Verfügung. Bei Reflektoren wird ein gewisser Teil dieser Fläche durch Fangspiegel abgeschattet. Als Fläche muß daher dort die effektive Fläche herangezogen werden.
L = Lichtsammelvermögen
D Teleskop = Durchmesser des Teleskopeffektives
D Fangspiegel = Durchmesser des Fangspiegels
DP = Augenpupille Durchmesser
Im folgenden Beispiel wollen wir wiederum ein SC mit einem Apo vergleichen:
Schmidt Casegrain:
D Teleskop = 8'' = 203,2 mm
D Fangspiegel = 63,5 mm
Dp = 7 mm
L = 760 fach
Apochromat:
D Teleskop = 100 mm
Dp = 7 mm
L = 204 fach
Wie überträgt man diesen Wert jetzt auf die reale Welt? Was kann beobachtet werden?
Dahingehend kann man das Lichtsammelvermögen in Magnitude umrechnen:
Zu diesem Wert muss noch die visuelle Grenzgröße hinzuaddiert werden. Für Städte beträgt diese ca. 4mag. Diese Zahl gibt vereinfacht gesagt an, was die Atmosphäre von sich aus noch sichtbar erscheinen lässt. Im Fall der Stadt sind es Objekte bis zur Größenklasse 4. Alles darüber hinaus wird durch Lichtverschmutzung, Smog usw. unsichtbar. Ländliche Gegenden haben einen höheren Wert und werden laut Wikipedia mit ca.6 bis 7 Magnituden angegeben. Wichtig hier: Je größer die Magnitude desto schwächer das Objekt.
Für unsere bereits behandelten Teleskope ergibt sich also:
Schmidt Casegrain:
D Teleskop = 8'' = 203,2 mm
D Fangspiegel = 63,5 mm
Dp = 7 mm
L = 760 fach
L mag = 7,2
Zuzüglich der Grenzgröße sichtbarer Objekte in Städten von 4 mag können also mit dem SC Objekte bis ca 11 Magnituden beobachtet werden.
Apochromat:
D Teleskop = 100 mm
Dp = 7 mm
L = 204 fach
L mag = 5,8
Zuzüglich der Grenzgröße sichtbarer Objekte in Städten von 4mag können also mit dem APO Objekte bis ca. 10 Magnituden beobachtet werden.