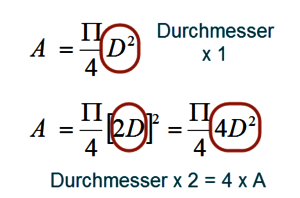2. Das Sichtbarmachen flächiger Objekte - Helligkeit der Abbildung
In den letzten Kapiteln wurde gezeigt, wie Objekte vergrößert werden. Einen Stern in der Unendlichkeit ist nicht vergrößerbar. Dazu muss man sich das Bild des Mondes vorstellen, welcher von seinem Nord- und Südpol je einen Mittelpunktstrahl aussendet. Jeder dieser Strahlen schneidet mit der Brennebene. Die Ausdehnung dieser zwei Punkte auf der Brennebene definiert den Durchmesser der Mondes im Zwischenbild.
Nähere ich Nord- und Südpol des Mondes soweit an, dass er zum Punkt wird, dann fallen beide Mittelpunktstrahlen zusammen. Somit entsteht nur ein Punkt (besser ein Beugungsscheibchen) in der Brennebene. Für das Darstellen eines flächenhaften Objektes fehlt die reale Ausdehnung.
Warum also ein Teleskop kaufen, wenn die Vergrößerung nicht die entscheidende Rolle spielt? In dem Satz steckt nur die halbe Wahrheit. Der Bildausschnitt, so wie ich ihn mit unbewaffneten Auge beobachte, wird vergrößert; die punktförmigen Objekte in diesem jedoch nicht. Um sich das besser vorstellen zu können ersetzt man den Mond der vorangegangenen Darstellung durch einen kreisförmigen Himmelsausschnitt mit Sternen. Der Bildausschnitt wird als Zwischenbild dargestellt. Die Sterne in diesem Bild bleiben punktförmig.
Über den Blickwinkel des Auges wird also ein Himmelsausschnitt beobachtet. Dieser Ausschnitt enthält eine Lichtmenge, welche auf diesen Ausschnitt verteilt ist. Mann könnte auch den Quotienten aus Lichtmenge und Himmelsausschnitt als Lichtdichte bezeichnen. Wenn ich es also schaffe, diese Lichtmenge enger zu bündeln (also die Lichtdichte erhöhe), dann müßte dem Augen ein Bild heller erscheinen. Dieser Zusammenhang wird durch die Austrittspupille beschrieben.
Zu allererst sollten wir uns aber kurz nochmals mit ein wenig Mathematik und Theorie beschäftigen.
Im Kapitel zum Thema Zwischenbild ist ein Punkt erwähnt wurden, welcher hier praktische Bedeutung erlangt und das ist der Punkt zur Größe des Zwischenbildes. Aus dem Strahlensatz ergab sich:
B = f / g x G
B = Zwischenbildgröße
f = Brennweite Teleskop
g = Objektabstand
G = Objektgröße
Eines fällt sofort auf! Wo ist in dieser Gleichung der Durchmesser des Objektives?
- Erste Erkenntnis aus der Gleichung ist also: Dieser spielt für die Größe des Zwischenbildes theoretisch und real keine Rolle.
- Zweite Erkenntnis aus der Gleichung ist, dass das bei ansteigender Brennweite des Teleskopes die Zwischenbildgröße (und damit die mögliche Vergrößerung) steigt.
- Dritte Erkenntnis ist, dass somit alle Teleskope mit gleicher Brennweite die gleiche Zwischenbildgröße abliefern müssen und dabei ist die Öffnung völlig uninteressant.
Jetzt kommt ein wichtiger Punkt ins Spiel: Je größer aber die Öffnung desto mehr Photonen (Licht) werden gesammelt.
Im Zusammenhang mit Erkenntnis Drei bedeutet das:
- Ein Telekop mit sehr großer Öffnung sammelt viel Licht und verteilt es bei einer Brennweite x auf eine Zwischenbildgröße y.
- Ein Teleskop mit kleinerer Öfnnung sammelt weniger Licht und verteilt es bei der gleichen Brennweite x auf die gleiche Zwischenbildgröße y.
Macht es bei Planetenbeobachtung nun Sinn eine sehr große Optik zu besitzen? Jein! Aus reiner Betrachtung zum Thema Licht gegebenenfall nicht, da Planeten bereits sehr helle Objekte sind! Beim näheren Betrachtung der Frage dann doch, da große Öffnungen meist mit langen Brennweiten verknüpft sind. Das führt zu großen, für Planetenbeobachtung sicher förderlichen, Vergrößerungen. Weiterhin ist auch das Auflösungsvermögen eines Teleskopes von der Öffnung abhängig. Will ich Strukturen auf Planeten entdecken, dann brauche ich große Öffnungen (siehe 4.)
Damit sind die Funktionen Brennweite und Öffnung abgegrenzt:
Die Brennweite ist für die Größe des Zwischenbildes zuständig (und damit der Vergrößerung)!
Die Öffnung ist für die Lichtsammelleistung verantwortlich, welche sich auf die Größe des Zwischenbildes verteilt.
- Wenn ich also in meiner oben aufgeführten Gleichung die Brennweite verdoppele, dann verdoppelt sich der Duchmesser des Zwischenbildes, was zu einer Vervierfachung der Fläche führt (siehe Gleichung am Ende der Seite).
Wir nehmen nun abschließend zwei Teleskope gleicher Öffnung. Dabei hat Teleskop B die doppelte Brennweite wie Teleskop A.
- Das führt zum Ergebnis, dass beide Teleskope ersteinmal das gleiche Lichtsammelvermögen (da gleiche Öffnung) haben. Teleskop A verteilt das Licht aber auf eine Fläche, welche 4x kleiner ist als die des Teleskopes B. Das Bild im Teleskop A ist kleiner und erscheint heller! Das Bild im Teleskop B ist größer und erscheint dunkler!
Obwohl nun beide Teleskope das gleiche Lichtsammelvermögen haben, scheint das kurzbrenn-weitigere hellere Bilder zu liefern. Hinsichtlich der Belichtungszeiten ist es damit "schneller". Das Teleskop mit der größeren Brennweite bei gleicher Lichtsamelleistung ist hinsichtlich Belichtungszeit nun "langsamer". Warum die gleiche Lichtmenge zu unterschiedlichen Belichtungszeiten führt, wird in einen folgenden Kapitel erklärt, welches noch in Vorbereitung ist.