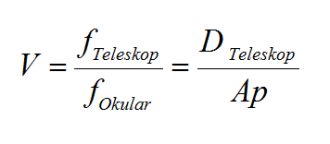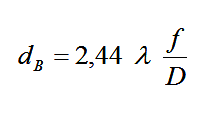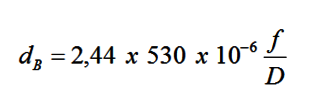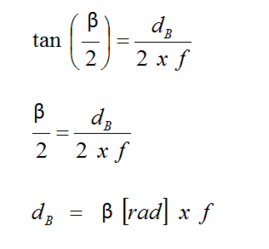Im vorangegangenen Artikel hatte ich mich mit der Flächenhelligleit von flächigen Objekten im Zwischenbild eines Teleskopes beschäftigt. Dieses Zwischenbild muß nun dem Auge zur Verfügung gestellt werden. 

Zwischen den Eckdaten eines Teleskopes (Brennweite Okular und Teleskop; Öffnung, Vergrößerung und Austrittspupille) existieren folgende Zusammenhänge:

V                 = Vergrößerung

f Teleskop   = Brennweite Teleskop

f Okular       = Brennweite Okular

D Teleskop  = Öffnungsdurchmesser Teleskop

Ap               =  Austrittspupille Okular = Lichtbündeldurchmesser, welcher aus dem Okular tritt

Aus der Gleichung erkennt man, dass die Vergrößerung mit steigender Teleskop- und fallender Okularbrennweite steigt. Im umgekehrten Fall sinkt die Vergrößerung mit fallender Teleskop- und steigender Okularbrennweite. Da Okulare variabel und somit tauschbar sind gilt:

• maximale Vergrößerungen werden mit Teleskopen großer Brennweite erreicht

Und trotzdem haben kleinere Brennweiten mindestens die gleiche Bedeutung und dies hängt damit zusammen, dass diese Teleskope kleinere Vergrößerungen möglich machen und so größere Bildausschnitte ermöglichen.  Was nutzt ein Ausschnitt einer Galaxie, wenn man keinen Bezug zum großen Ganzen hat.

• Je kleiner die Vergrößerung desto heller erscheinen die Objekte im Okular bei damit verbundenem größeren Bildausschnitt. Gleichzeitig scheint  aber auch die Helligkeit des Hintergundes und die Abgrenzung von Objekt und "aufgehellten" Himmel wird schwieriger. 

• Je größer die Vergrößerung, desto dunkler erscheinen die Objekte im Okular bei sinkendem Bildausschnitt. Gleichzeitig sinkt die Helligkeit des Hintergrundes und lichtschwache Objekte können sich besser abgrenzen. Für das Sichtbarmachen von lichtschwachen Objekten haben Vergrößerungen also auch Ihre Berechtigung obwohl z.B. Sterne nicht vergrößerbar sind.

Um das zu illustrieren anbei die maximale und minimale Vergrößerung anhand eines Beispiels erklärt::

Es scheint nur logisch, dass man die im vorangegangenen Artikel erwähnten Zwischenbilder nur vergrößern muß. Warum dann das Spiel mit den Öffnungen und Brennweiten? Egal  wie groß das Zwischenbild ist, das Okular (die Lupe) wird es schon richten! Nicht ganz, hier kommt wieder das Licht und dessen Beugung ins Spiel.

Wir wählen zwei typische Teleskope

• Schmdt Casegrain mit 8" Öffnung (203,2 mm) und  2032mm Brennweite also ein Teleskop mit großer Öffnung und langer Brennweite; ideal für große Vergrößerungen
• Apochromat mit 100mm Öffnung und 600mm Brennweite also ein Teleskop mit geringer Öffnung und kurzer Brennweite; ideal für ausgedehnte Himmelsobjekte

Wie groß ist die förderliche Vergrößerung eines Teleskopes?

Die förderliche Vergrößerung eines Teleskopes ist physikalisch und anatomisch begrenzt.

Die erstere Grenze wird durch das Auflösungsvermögen eines Teleskopes gebildet. Selbiges ist der kleinste Abstand zwischen zwei beobachteten Objekten in der Brennebene eines Teleskopes, welcher tatsächlich als Abstand identifiziert, d.h. aufgelöst werden kann. Diese Distanz enstpricht dem Radius eines Beugungsscheibchen, dem sogenannten Rayleigh Kriterium, welches im Kapitel 4 näher erklärt wird. Der Abstand wird dabei in Winkelsekunden angegeben und ist winzig. Bei einem Teleskop mit 90mm Objektivdurchmesser würde die Grenze des Darstellbaren bei 1,3" erreicht werden.

Das menschliche Auge hat selbst ein Auflösungsvermögen von ca. 180". Das heißt, um die Auflösung oder den Abstand der zwei Objekte in der Brennebene für das Auge sichtbar zu machen, muss ich diese Distanz (im Beispiel 1,3") so vergrößern, dass ihn das menschliche Auge als Abstand unter 180" erkennt. Diese Grenze wird also durch die Anatomie gezogen und stellt die förderliche Vergrößerung dar.

Was würde passieren, wenn ich weiter vergößere? Kleinere Details als die beschriebene Distanz (im Beispiel 1,3") kann mein Teleskop nicht darstellen. Also warum dann weitervergrößern?  Es werden keine weiteren oder feineren Details sichtbar werden, denn ich sehe bereits  das Maximum an Informationen.

Es besteht aber die Möglichkeit auf größere Teleskope auszuweichen, denn die Auflösung des Teleskopes ist von dessen Durchmesser abhängig. Aber Vorsicht! Durch atmosphärische Störungen wird die Auflösung begrenzt. Was nutzt eine große Auflösung, wenn die Luftunruhe das theoretisch Erreichbare zunichte macht. Diese atmosphärische Grenze liegt bei ca. 1". Hinsichtlich Auflösung würde ein Teleskop mit theoretisch über 133mm Öffnung keinen Gewinn mehr bringen es sei denn ich platziere es in den Anden :-)!

Nimmt man nun diese Vergrößerung als Basis, kann man ausrechnen, welche Austrittspupille dann erreicht wird. Sie liegt bei jedem Teleskop, d.h. unabhängig dessen Größe, bei ca. 0,70mm. Warum dies so ist, wird am Ende dieser Seite als kleiner Anhang dargestellt:

Für den Durchmesser des Beugungsscheibchens (bis zum ersten Helligkeitsminimum) und dessen Radius gilt:

• Lambda   =     Wellenlänge des sichtbaren Lichtes
• f                =     Brennweite Teleskop
• D              =     Durchmesser Objektiv 

für das sichtbare Licht kann eine durchschnittliche Wellenlänge von 530nm also 530x10^(-6)mm angenommen werden.

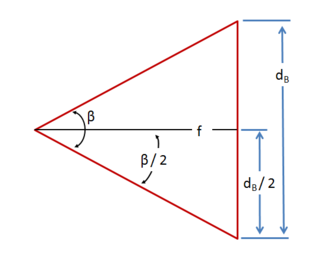
Das Beugungsscheibchen entsteht im Zwischenbild des Teleskopes. Bei kleinen Winkeln kann der Tangens des Winkels durch den Winkel selbst, da identisch, ersetzt werden. Somit ergibt sich die Größe des Beugungsscheibchen nun auf das Zwischenbild bezogen.

Diese Gleichung setzen wir nun in die erste Gleichung ein. Dabei kürzt sich die Brennweite. Der Winkel in Radiant wird erst in Grad (180/PI), dann in Minuten (60'/1° x 60''/1') gewandelt.

Wir nehmen nun also unsere zwei Optiken und berechnen die Teleskopauflösung (was nach Rayleigh dem Radius entspricht)

Schmidt Cassegrain:

Radius Beugungsscheibchen = 0,5 x Beta [''] =  133 / 203,2 = 0,65

Apochromat

Radius Beugungsscheibchen = 0,5 x Beta [''] = 133 / 100,0 = 1,33

Wie erwähnt errechnen wir nun die förderliche Vergrößerung anhand des Verhältnisses des Auflösungsvermögen des Auges (180'') zur Größe des Beugungsscheibchens:

Schmidt Cassegrain:

V = 180'' / 0,65'' = 277 fach

Apochromat:

V = 180'' / 1,33'' = 135fach

Mit der Gleichung  Ap = D / V ergibt sich nun die  Austrittspupille für die förderliche Vergrößerung:

Schmidt Cassegrain:

Ap = 203,2 mm  /  277 =  0,73

Apochromat:

Ap = 100,0 mm  /  135 = 0,74

Damit ist die Austrittspupille für förderliche Vergrößerungen definiert. Sie liegt ca. bei 0,7mm.

Was sich hieraus ableitet: Die förderliche Vergrößerung ist ein Wert, welcher den Faktor Mensch mit beinhaltet!

Die minimalen Vergrößerungen hingegen bedingen maximale Austrittspupillen, wobei hier die Öffnung der Augenpupille des Menschen die Grenze setzt. Diese liegt bei ca. 7mm. Eine Überschreitung dieses Wertes bedeutet, dass Licht an der Pupille ungenutzt vorbeifließt.

Die maximalen Helligkeiten von Objekten im Okular bei unterschiedlichen  Objektivgrößen  (d.h. die maximale Helligkeit eines Objektes im Okular = Ap 7mm) sind theoretisch mit beiden Teleskopen erreichbar.

Beim SC Teleskop müsste dazu die Vergrößerung auf 29fach reduziert werden. Beim Apo wird die maximale Lichtausbeute im Okular des gleichen Objektes bei 14facher Vergrößerung erreicht. Dabei ist aber von Bedeutung, dass der Apo dies durch den Einsatz eines handeslüblichen 40mm Okulars annähernd schafft. Ein 70mm Okular wie beim SC hingegen gibt es nur in der Theorie.

Maximale Helligkeiten erreichen wir also mit 7mm Austrittspupille, wobei entsprechend der Gleichung V = D / Ap bei gleicher Austrittspupille das Teleskop mit der größeren Öffnung eine höhere Vergrößerung erreicht.  Das Gehirn interpretiert das größer vergrößerte gleich hell dargestellte Objekt, als heller.

Im Umkehrschluss schafft unser SC zwar nicht die 7mm sondern nur eine 4mm Austrittspupille dies aber bei 51facher Vergrößerung. Das Objekt kann durchaus vom Gehirn trotzdem ähnlich hell interpretiert werden wie beim Apochromat mit maximal 6,7mm Austrittspupille und lediglich 15facher Vergrößerung. Dabei liefert der Apo aber rein physikalisch das hellere Bild. 

Die 7mm Ap lässt nicht nur das Objekt heller erscheinen, sondern auch die Lichtverschmutzung. Meist ist eine kleinere Austrittspupille im Vorteil, da kontrastreicher. Ein sehr helles Objekt vor hellem Hintergrund ist kontrastseitig einem dunkleren Objekt allerdings vor schwarzem Hintergund unterlegen.

Ganz sicher ist aber beim Apochromaten der Vorteil des großen Gesichtsfeldes, da er kleiner vergrößern kann. Ausgedehnte Galaxien werden bildfüllend ablichtbar. Das SC kann unter Umständen nur einen unbefriedigenden Ausschnitt liefern, da es es in seiner minimalen Vergrößerung limitiert ist.

Nur Mathematik langt hier alleine nicht. Entscheidend ist, wie interpretiere ich die Ergebnisse.

Um ein Teleskop also einschätzen zu können,  benötigt man einen Wert, welcher dieses Verhalten umschreibt. Dieser Wert ist das:

• Öffnungsverhältnis

Die Formel entstand aus der Gleichung für die Berechnung der Vergrößerung am Anfang der Seite. Man erkennt, dass die Ap steigt (die Belichtungszeit sinkt) je größer das Öffnungsverhältnis ist. 

Bitte beachten, dass zwar 10 größer 6 ist aber 1/10 kleiner 1/6 ist. Unser Apochromat hat also das größere Öffnungsverhältnis! Ooooh ja ;) 

Für unser SC Teleskop wäre die Öffnungszahl:

203,2mm / 2032 mm = 0,10 = 1/10 = f/10

Für unseren APO wäre die Öffnungszahl:

100mm / 600mm = 0,17 = 17/100 = 1/5,88 = rund 1/6 = f/6                   (17/17 = 1 und 100/17=5,88)

Für Interessierte anbei wie oben erwähnt die Erklärung, warum die minimale Austrittspupille unabhängig von der Teleskopöffnung ist.

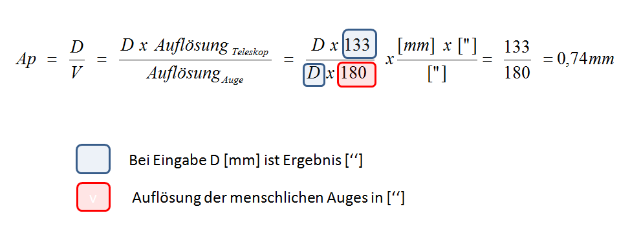
Basis ist die Formel für die Austrittspupille. Die förderliche Vergrößerung ersetze ich durch das Verhältnis des Auflösungsvermögen von Auge zu Teleskop. Letzteres kann ich durch die größenangepasste Radiengleichung des Beugungsscheibchen (133/D) ersetzen. Die Durchmesser kürzen sich im Wert heraus aber nicht deren Einheit. Am Ende steht eine Konstante (133), welche durch die 180" Auflösung des Auges geteilt wird. Und das Ergebnis ist unabhängig vom Durch-messer.